La quale converge ad una radice se 
L’errore 
dove r � la radice esatta , ha la propriet� :
Ricerca Di Equazioni Nel Campo Reale
Un
problema molto importante dell’analisi matematica � quello di trovare radici di
equazioni .
Noi supporremo di considerare
funzioni reali f(x):R� R ,voglio trovare una soluzione per f(x):=0.
Effettueremo un ragionamento che
parte dal supporre che esista almeno una soluzione e che f(x) sia continua e derivabile .
Come riusciremo ben a comprendere in seguito tutti gli algoritmi che studieremo si basano
sull’iterazione in quanto i metodi diretti sono di interesse solo nei casi pi�
semplici (fino al secondo grado). A lezione ci siamo accorti che i metodi iterativi
presentavano dei problemi :
1-La procedura deve essere
ben definita (la successione delle iterate deve rimanere nel dominio
della
funzione di iterazione)
2-Il metodo deve convergere
3-Il costo della procedura non
deve essere alto(in termini di tempo)
Prima di svolgere
l’esercizio disegneremo sempre in grafico della funzione f(x) per capire
approssimativamente dove i suoi zeri sono localizzati , questo ci serve anche per vedere
che la procedura da noi realizzata funzioni correttamente dandoci per risultati i valori
aspettati.
Un’altra ipotesi che
facciamo � che sia possibile separare le radici , cio� che sia possibile costruire
intervalli privi a 2 a 2 di punti in comune altrimenti il metodo iterativo pu� fallire .
In questo contesto possiamo considerare :
1--Il metodo iterativo ;
2--Il metodo di Newton ( o
della tangente);
3--Il metodo delle secanti
;
4--Il metodo della
dicotomia ;
5--Il metodo delle rette
parallele;
Il metodo da usare dipende dal
fatto che interessino tutte le radici di una particolare equazione o solo alcune , che le
radici siano reali o complesse , semplici o multiple , che si possieda una prima
approssimazione o no , e cos� via .
Ma andiamo con ordine:
Risolve eq. del tipo x :=F(x) per mezzo della formula di ricorrenza
La quale converge ad una radice se
L’errore dove r � la radice esatta , ha la propriet� :
Comprendiamo quindi che ad
ogni iterazione l’errore si riduce di un fattore prossimo ad F’(r).
Se F’(r) � prossimo
all’unit� allora ci vorranno un gran numero di iterazioni per ridurre l’errore
Ci� causa di una lenta
convergenza.
2. Il metodo di Newton (o delle tangenti)
Supponiamo di
porci nelle ipotesi sopra esposte. Il metodo delle tangenti ha un immediata
interpretazione geometrica ,infatti esso corrisponde ad usare la retta tangente alla
nostra funzione y=f(x) nel punto 
al posto della curva
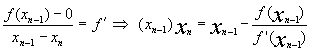
Pertanto
questa � la formula ricorsiva che il metodo di Newton usa per risolversi.Questo metodo �
migliore del precedente in quanto converge pi� rapidamente e di solitoraggiunge lo scopo
; esso � caratterizzato da un errore del tipo: 
Questa espressione � nota
come convergenza quadratica e testimonia quanto sopra detto infatti
Mostra che il numero di cifre
esatte si raddoppia quasi ad ogni iterazione.
Differentemente dal primo questo metodo non richiede di determinare derivate . Il metodo consiste nel fornire due stime iniziali x0 e x1 e poi calcolare la successione:
Dove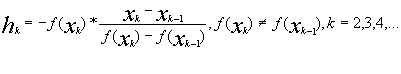 
Da osservare che geometricamente il punto 
� lo zero della retta passante per i
punti
Questo metodo consiste nel focalizzare le radici della nostra equazione mediante la tabulazione della funzione stessa. Supponiamo di aver trovato che la radice della nostra equazione cada all’interno dell’intervallo [a,b] suddivideremo ancora questo intervallo in sottointervalli ancora pi� piccoli , la radice della nostra equazione cade ora all’interno di [c,d] .Procederemo con il ragionamento sopra enunciato fino a quando non si raggiunge il grado di approssimazione voluto o il sistema non si blocchi
5. Il metodo delle rette parallele
Tale metodo consiste nel costruire una retta con coefficiente angolare fisso che parte ogni volta da un punto diverso. Iniziamo con quello d’intersezione con l’asse e costruiamo una retta con lo stesso coefficiente. Pongo
La retta che
si costruisce � 
Ponendo y=0 otteniamo la formula ricorrente per il metodo delle rette parallele
Per comprendere meglio la
validit� dei cinque metodi sopra esposti abbiamo elaborato altre e tante funzioni
eseguite da Mathematica 3.0 . Ogni funzione � stata strutturata in modo da poter
scegliere il numero di iterazioni e la precisione interna; le variabili sono state
dichiarate localmente, per poterne aumentare la esportabilit�.
Il range su cui sono state fatte
lavorare le singole procedure � stato determinato per via grafica ed � lo stesso per
tutte e cinque.
Infine, risultati sono stati
importati in Execel 97 per una migliore analisi e veste grafica.
Esaminiamo i vari casi
1-Nell’anno 1225 Leonardo Pisano Studi� l’equazione :
e ricav� x=1,368808107 .Nessuno
conosce con quale metodo Leonardo trov� questo valore, ma � un risultato notevole per il
suo tempo. Abbiamo voluto verificare la bont� del risultato attraverso Mathematica 3.0
;ogni funzione � stata iterata ventiquattro volte e la precisione del risultato � stata
fissata a dodici cifre decimali. Come si pu� vedere, ed era prevedibile, il metodo pi�
efficiente � risultato quello di Newton che con solo
quattro iterazioni ci fornisce la
soluzione che trov� Pisano.
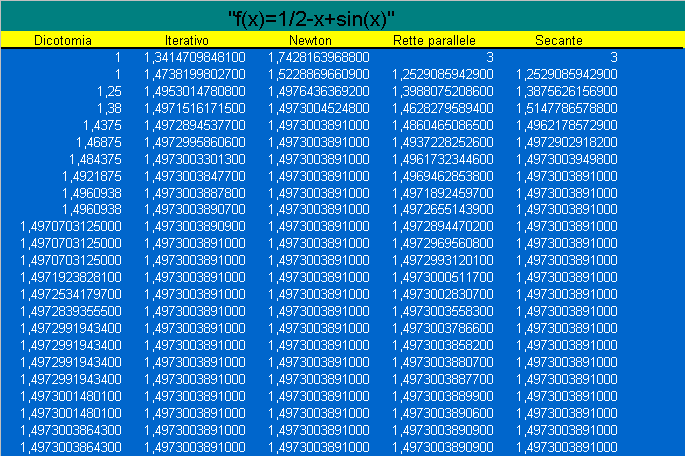
2-Calcoliamo una
radici dell’equazione 
come � possibile vedere dal grafico
l’equazione presenta una soluzione nell’intervallo (1,2) .
La funzione built-in di Mathematica
FindRoot ci d� come risultato:{x->1,49730045247996219} e anche questa volta
l’algoritmo di Newton � risultato pi� accurato.
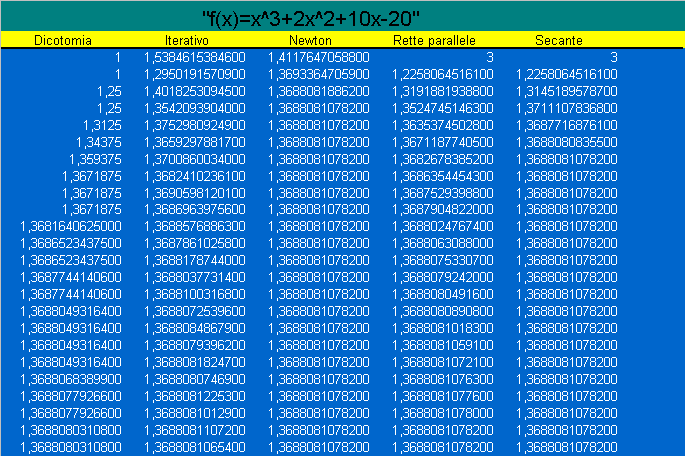
3- Ed infine consideriamo la funzione trascendente :
ricavando sempre dal grafico gli
estremi di interesse; FindRoot ci d� come soluzione
{x->2,64549772280714057}.
